megansa.blogg.se

The most commonly used version of the Student t-test effect size, comparing two groups ( \(A\) and \(B\)), is calculated by dividing the mean difference between the groups by the pooled standard deviation. There are multiple version of Cohen’s d for Student t-test. paired t-test (also known as dependent t-test or matched pairs t test).two-sample t-test (also known as independent t-test or unpaired t-test).We will provide examples of R code to run the different types of t-test in R, including the: T-test conventional effect sizes, proposed by Cohen, are: 0.2 (small effect), 0.5 (moderate effect) and 0.8 (large effect) (Cohen 1998).

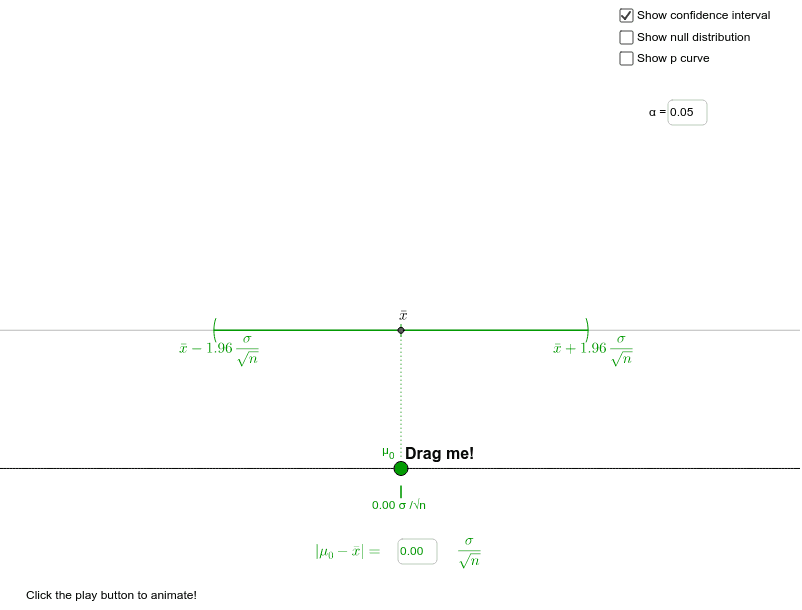
The d statistic redefines the difference in means as the number of standard deviations that separates those means.

t.test() : R base function to conduct a t-test.The result is a data frame, which can be easily added to a plot using the ggpubr R package. t_test() : a wrapper around the R base function t.test().Perform a t-test in R using the following functions :.I also consider it bad practice to calculate confidence intervals on groups as small as this, but I don't want to elaborate too much on this here.This article describes how to do a t-test in R (or in Rstudio). In practice it is often very close your homework problem explicitly asks for difference of means. It also tests a different hypothesis than difference of the means. A Wilcoxon test does also not circumvent the possible problem of bimodality in one of the sets. But they would urge caution and further investigation (if this were not a homework problem).Īll this together means a simple t-test would be a bad idea. Note that both of these observations might be a fluke given your small sample size. So either the other values give a bad estimate of the standard deviation or it is an outlier. And the second set of values seems to have one value which is considerably smaller than the others. This could be caused by two different sublocations or other differences between the shops. However, if I got those values two things would immediately attract my notice: the first set of values looks suspiciously bimodal. Your sample size is also too small to really check for normality. While this is obviously a homework question which wants you to do a t-test (more details on that if you show some effort yourself!), I want to add some practical concerns.įirst off, doing the t-test assumes normality and with your sample size you can not even assert robustness.